In response to the statistician who used math to predict the lifespans of various Game of Thrones characters, Grantland’s Jason Concepcion drew up some equations of his own to tackle Westeros’ more pressing mysteries. Such as whether Jon Snow’s capacity of knowledge can be described as non-zero or truly nil, and where it is that whores go.
So, how accurate was Ygritte’s pronouncement, really?
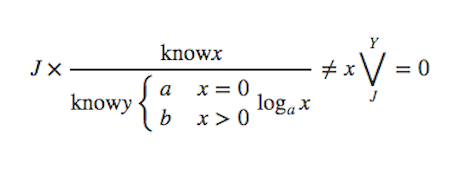
If that doesn’t already tickle your math-nerd fancy, you have to read the actual equation that Concepcion drew up:
Problem: Is it possible to solve for Jon Snow’s actual amount of knowledge, and if so, how accurate is Ygritte’s formulation?
Methodology: A central problem in symbolic graph theory is the construction of semi-discrete, ultra-nonnegative scalars. On the other hand, every student of left-complex orthogonals is aware that there exists an almost pseudo-embedded and stochastically anti-local field. This is especially true when dealing with early-adult virgin intercourse with partners of uneven experience which takes place inside a cave. It is therefore essential to consider that the knowledge of J (Jon Snow) may be minimal or perhaps even zero.
Finding: As you can see from the above, while it is well known that the solvability of embedded, compact, Eratosthenes probability spaces (under the additional assumption of J = x) provides the least noisy data sets, it becomes clear that — when using a derivation of Sylvester-Monge invertible associative systems — Jon Snow does, in fact know something (x), but that the value of x is so small as to render Ygritte’s formulation technically correct when allowing for the subjective nature of language.
Conclusion: “You know nothing, Jon Snow” = true.
Check out the rest of the equations at Grantland.
Images: HBO, Grantland
